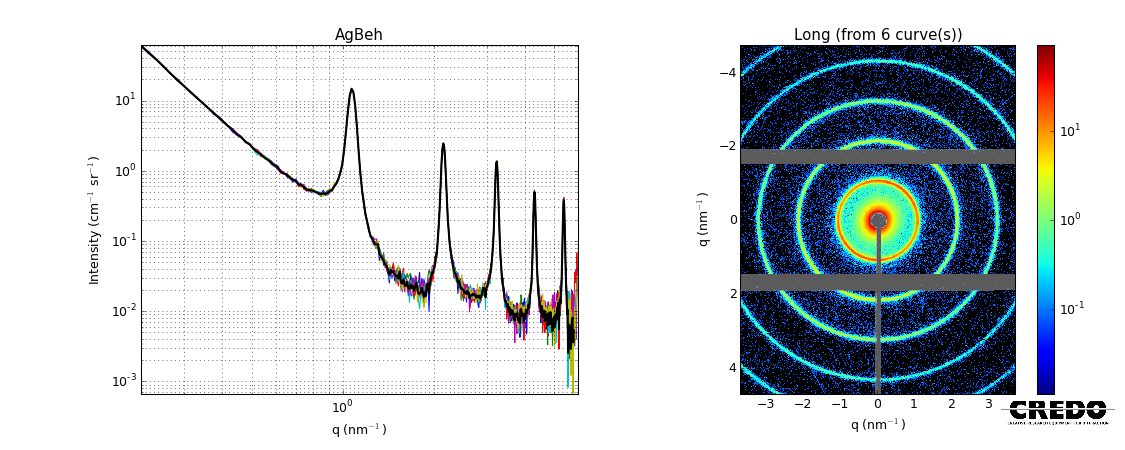
Bragg peaks
If some sort of periodicity on the resolvable size range is present in the sample under investigation, usually many orders of relatively sharp peaks manifest themselves in the scattering pattern. This can be understood as a special case of the scattering, the so-called Bragg-reflection principle.

According to the classic description in wide-angle X-ray diffraction, radiation coming from the X-ray source is reflected by crystal planes, and is detected by a single-channel detector placed far apart the sample in such a way, that the incidence and the exit angle are the same (left part of the figure above). If the optical path differences between rays reflected from subsequent layers is integer times the wavelength, the two rays arrive at the detector in phase, thus constructive interference occurs. This is formalized by the Bragg equation:
$$2 d \sin{\theta} = n\lambda \quad \textrm{where}\quad n \in \mathbb{N}\textrm{,}$$
$d$ being the periodicity of the crystal, $\theta$ the incidence and exit angle and $\lambda$ the wavelength. This formula can be expressed in a simpler form by using the $q$ scattering variable:
$$q = \frac{2\pi n}{d} \quad \textrm{where}\quad n \in \mathbb{N}\textrm{.}$$
The direct result of these equations is the occurrence of sharp peaks in the diffractograms of crystals, found at those $2\theta$ scattering angles, where the criterion is fulfilled. The right side of the figure above symbolizes that to fulfill the Bragg criterion, one does not need to have crystalline order, just some kind of discrete translational symmetry. For example, in case of equidistantly ordered lamellae, as found in silver behenate or multilamellar phospholipid vesicles, can also yield Bragg-like peaks in the scattering curve. Silver behenate contains such lamellae, spaced ~5.8 nm apart, and as a consequence, Bragg peaks are manifested in its small-angle scattering curve.