The Guinier approximation
The study of the shape and size distribution of nanoparticles is a traditional field of application of SAXS. The scattering intensity of a spherical particle of radius $R$ and homogeneous scattering length density $\Delta\rho$ inside it, for example, can be calculated as
$$I_\mathrm{sphere}(q)=\Delta\rho^2 V_\mathrm{sphere}^2\left[\frac{3}{(qR)^3}\left(\sin\left(qR\right)-qR\cos\left(qR\right)\right)\right]^2\textrm{,}$$
where $V_\mathrm{sphere}$ is the volume of the particle. The scattering curves of spheres with different radii are plotted in the figure below.
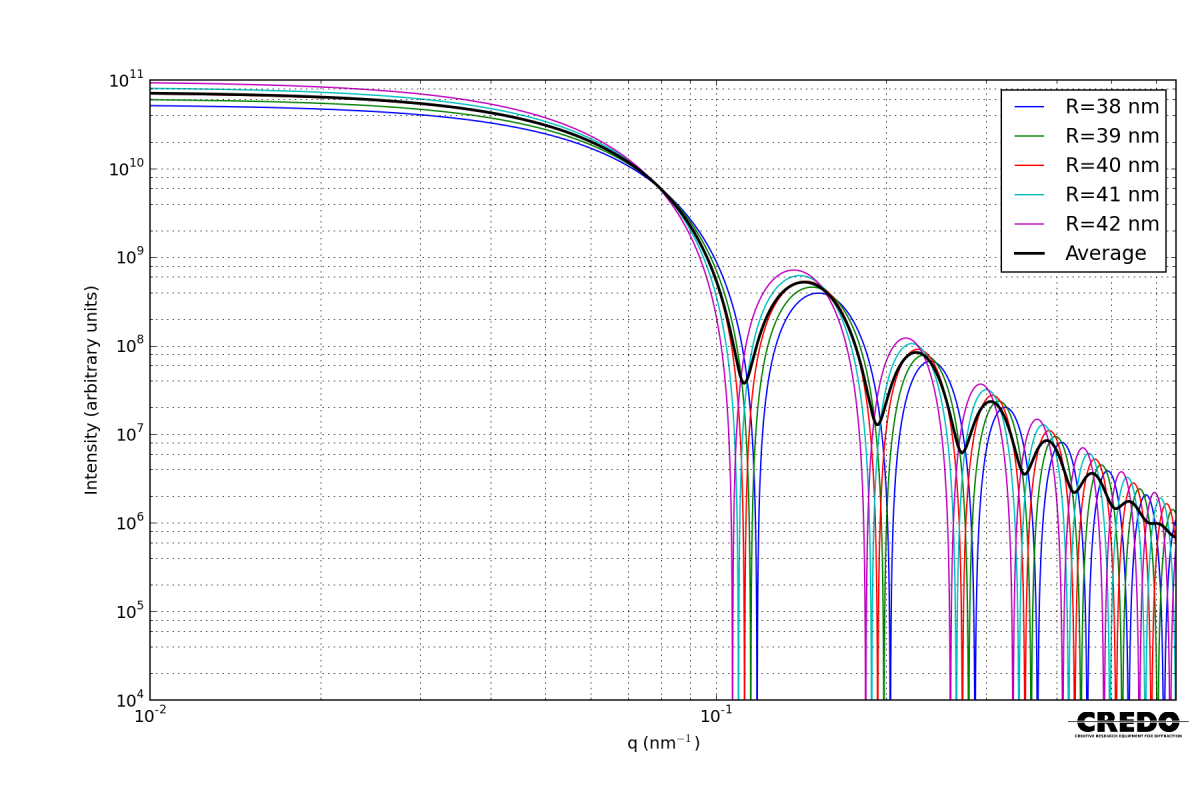
The scattering curve starts with a slight bend at small $q$ values, and levels to a constant value at $q \approx 0$. This constant is $I(0)=V_\mathrm{sphere}^2\Delta\rho^2$, i.e. the square of the total scattering length (roughly speaking the total number of electrons) inside the particle. This enables one to determine an average molecular weight if our approach is extended to solutions of globular macromolecules.
The small-$q$ limit of the scattering curve is a Gaussian curve, centered to the origin:
$$I(q \gtrapprox 0) = I(0) e^{-\frac{q^2R^2}{5}}\textrm{.}$$
This formula can be generalized to any form of scattering particle, including disks, rods, even non-homogeneous scattering length densities. It can be proven that the above equation, the so-called Guinier approximation holds in this case, too, in the following form:
$$I(q \gtrapprox 0) = I(0) e^{-\frac{q^2R_G^2}{3}}\textrm{.}$$
The only difference is that instead of $R$, we have $R_G$, the radius of gyration or Guinier radius, which is defined for an arbitrary scattering particle as
$$R_G=\sqrt{\frac{\iiint \Delta\rho(\vec{r})r^2\mathrm{d}\!\vec{r}}{\iiint \Delta\rho(\vec{r})\mathrm{d}\!\vec{r}}}\textrm{,}$$
where the domain of the integrals is the whole irradiated volume. This complex formula reduces into usually much simpler forms with the knowledge of the form of the scattering particle. For instance in the case of spheres, $R_G=\sqrt{3/5}R$ holds.
